The (a – b)^3 formula is used to find the cube of a binomial which is made up of the difference of two terms. It says (a – b)3 = a3 – 3a2b + 3ab2 – b3. This is one of the algebraic identities.
This formula is used to calculate the cube of the difference between two terms very easily and quickly without doing complicated calculations. Let us learn more about a minus b whole cube formula along with solved examples.
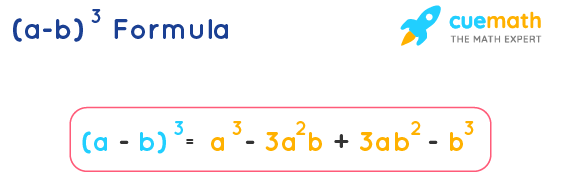
What is the (a – b)^3 Formula?
The (a-b)^3 formula is used to calculate the cube of a binomial. The formula is also known as the cube of the difference between two terms. According to “a minus b whole cube formula”,
(a – b)3 = a3 – 3a2b + 3ab2 – b3 (or) a3 – b3 – 3ab (a – b)
We can derive this formula in two ways:
- Method 1: By expanding (a – b)3 as (a – b) (a – b) (a – b).
- Method 2: By using the formula of (a + b)3
Derivation of (a – b)^3: Method 1
To find the formula of (a – b)3, we will just multiply (a – b) (a – b) (a – b).
(a – b)3 = (a – b)(a – b)(a – b)
= (a2 – 2ab + b2)(a – b)
= a3 – a2b – 2a2b + 2ab2 + ab2 – b3
= a3 – 3a2b + 3ab2 – b3 (or)
= a3 – b3 – 3ab (a – b)
Therefore, (a – b)3 formula is:
(a – b)3 = a3 – 3a2b + 3ab2 – b3
Hence proved.
